Contents
公式
定义:
h(n)=\sum_{i=0}^{n-1}h(i)b(n-1-i)
生成函数:
F(x)=xF^{2}(x)+1=\frac{1-\sqrt{1-4x}}{2x}
性质:
\begin{aligned}
h(n)&=\frac{\binom{2n}{n}}{n+1}\cr h(n)&=C_{2n}^n-C_{2n}^{n-1}\cr h(n)&=h(n-1) * \frac{4n-2}{n+1}\cr
\end{aligned}
前几项:
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, \cdots
经典应用
出栈序列问题
n 个不同的数依次进栈,求不同的出栈结果的种数?
二叉树同构计数问题
n 个结点可够造多少个不同的二叉树?
路径计数问题
- 如左图,在 m * n 的方格地图中,从一个角到另一个角(成对角线),不跨越对角线的路径数为多少?
从反面考虑问题。设 M 为穿过直线 y=x(表示会经过直线上方的点)的从 O\to P 的路径组成的集合,如中图。利用对称可以将 M 中第一次犯规时的路径对称,然后再将剩下的部分接在对称后的路径上,由于此时将一次向上移动修改为了向右移动,因此终点由变成了 P’,此时就建立了与 O 到 P’ 的路径的一个一一映射。
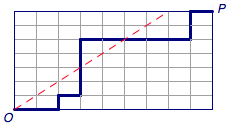
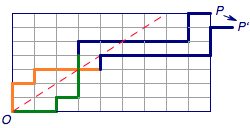
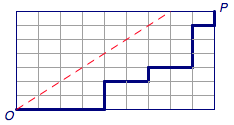
于是所求的排列数为C_{m+n}^{n}-C_{m+n}^{n-1},当 m=n 时即为卡特兰数。
- 从 (0,0) 到 (n,n) 的除端点外不接触直线 y=x 的非降路径数:
先考虑 y=x 下方的路径,都是从 (0,0) 出发,经过(1,0)及(n,n-1)到(n,n),可以看做是(1,0)到(n,n-1)不接触y=x的非降路径数。
所有的的非降路径有C_{2n-2}^{n-1}条。对于这里面任意一条接触了y=x的路径,可以把它最后离开这条线的点到(1,0)之间的部分关于y=x对称变换,就得到从(0,1)到(n,n-1)的一条非降路径。反之也成立。从而y=x下方的非降路径数是C_{2n-2}^{n-1}-C_{2n-2}^{n}。根据对称性可知所求答案为2C_{2n-2}^{n-1}-2C_{2n-2}^{n}。
圆内连弦问题
如图,圆周上有 2n 个点,以这些点为端点连互不相交的 n 条弦,求不同的连法总数.
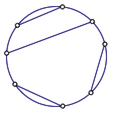
- 辅助问题:
圆周上有 2n+1 个点,其中 n+1 个点上标“+1”,n 个点上标“-1”,如果可以找到某个标有“+1”的点作为起点,当顺时针沿圆周前进时将所遇到的点(包括起点)上标的数相加得到的和始终为正数,就称这种标记法是好标记法.求好标记法的总数(注意考虑圆排列)
- 辅助问题的解:
对于任何一种标记法,我们将顺时针相邻的“+1”“-1”(指顺时针前进时先遇到“+1”后遇到“-1”)同时抹去,可以证明抹去的前后对标记法的好坏没有影响.不停的重复这一过程,则最后只剩一个标有“+1”的点,显然此时标记法为好的.因此所有的标记法都是好标记法,显然其数目为:
\frac{1}{2n+1}C_{2n+1}^{n}=\frac{C_{2n+1}^{n}}{2n+1}
- 问题的解:
通过对辅助问题的进一步探索可知,每一种将圆周上2n+1个点标记为n+1个”+1“点,和n个”-1“点的方法唯一确定一个顺时针前进的方案(即起点).我们将这个起点删去,剩下的2n个点在顺时针方向上一定为“+1”“-1”“+1”“-1”,…,此时将顺时针相邻的这些“+1”“-1”点用弦连接起来,就得到互不相交的条弦.这样我们就建立了从好标记法到弦的连法的单射.
反过来,如果我们有了一种弦的连法,就可以从某条弦的端点出发顺时针前进,对每条弦的两个端点都是先遇到的端点标上“+1”,后遇到的端点标上“-1”,然后在最后回到出发点时添上一个标有“+1”的点.这样我们就建立了从弦的连法到好标记法的单射.
综上,所求的不同连法数为
\frac{1}{2n+1}C_{2n+1}^{n}=\frac{C_{2n+1}^{n}}{2n+1}
凸多边形的剖分问题(卡特兰问题)
求凸 n+2 边形用其 n-1 条对角线分割为互不重叠的三角形的分法总数.
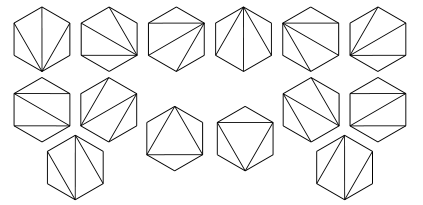
引理一:由 n 对括号形成的合法括号表达式的个数为 C_n.
引理二:n 个数连乘,不同的乘法顺序数为 C_n.
用 1,2,3,\cdots ,n+2 标记凸 n+2 边形的边,从标记为 1 的边的起点(按逆时针方向)开始按未标记的对角线均为向外标记方向,如下图:
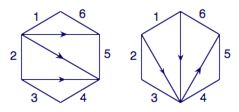
逆时针读图,将出的箭头读为左括号,进的箭头读为右括号,就得到了剖分方式与连乘顺序的对应.图10中的两个图对应的连乘顺序表达式分别为:1((2(34))5)6, (1(23))(45)6。抛开 6 不计,每个连乘顺序表达式实际上就是规定了 n+1 个数连乘时,不同的乘法顺序,根据引理一,得到剖分方式的总数为 C_n.