最大权闭合子图
定义:有一个有向图,每一个点都有一个权值(可以为正或负或 0),选择一个权值和最大的子图,使得每个点的后继都在子图里面,这个子图就叫最大权闭合子图。
解法:
这个问题可以转化为最小割问题,用网络流解决。
从源点 S 向每个正权点连一条容量为权值的边,每个负权点向汇点 T 连一条容量为权值的绝对值的边,有向图原来的边容量全部为无限大。求它的最小割,割掉后,与源点s连通的点构成最大权闭合子图,权值为 正权值之和 - 最小割。
可以理解为,所有点要么和 S 相连,要么和 T 相连(没必要全割掉)。割掉 S 与 i 的边,表示不选择 i 点作为子图的点;割掉 i 与 T 的边,表示选择 i 点为子图的点。
题目大意:
有 m 个实验,每个实验只可以进行一次,但会获得相应的奖金,有 n 个仪器,每个实验都需要一定的仪器,每个仪器可以运用于多个实验,但需要一定的价值,问奖金与代价的差的最大值是多少?
分析:
每个实验有正权值,仪器有负权值,从实验向所需要的仪器连边,问题即转化为求最大权闭合子图。
平面图最小割
例题:P4001 [ICPC-Beijing 2006]狼抓兔子
题目大意:
给一个如下的平面图,求最小割。
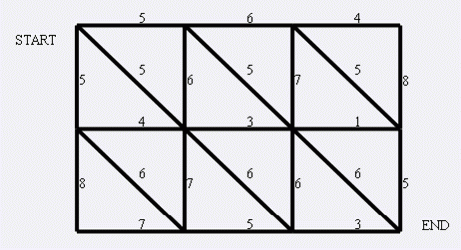
第一行两个整数 N,M,表示网格的大小。接下来分三部分。第一部分共 N 行,每行 M-1 个数,表示横向道路的权值。第二部分共 N-1 行,每行 M 个数,表示纵向道路的权值。第三部分共 N-1 行,每行 M-1 个数,表示斜向道路的权值。
分析:
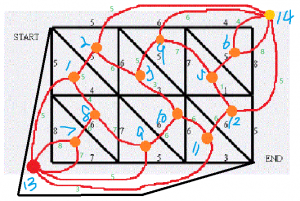
平面图的最小割等于其对偶图的最短路:我们先连接原先的起点和终点,然后对于每对相邻的块连边,权值和原图中相邻的边一样。连接 S 和 T 所形成的两块,其中的两点之间最短路即为答案。
此题注意特判 n=1 的情况,应直接连接 S 和 T。
int n, m, S, T;
int id(int x, int y, int op) {
return (x - 1) * (m - 1) * 2 + 2 * y - op;
}
int main(int argc, const char * argv[]) {
scanf("%d%d", &n, &m);
S = (n - 1) * (m - 1) * 2 + 1; T = S + 1;
for (int i = 1; i <= n; i++) {
for (int j = 1, w; j < m; j++) {
scanf("%d", &w);
if (n == 1) {
add(S, T, w); add(T, S, w);
continue;
}
int u = id(i, j, 0), v = id(i - 1, j, 1);
if (i == 1) {
add(u, T, w); add(T, u, w);
}
if (i == n) {
add(v, S, w); add(S, v, w);
}
if (i != 1 && i != n) {
add(u, v, w); add(v, u, w);
}
}
}
for (int i = 1; i < n; i++) {
for (int j = 1, w; j <= m; j++) {
scanf("%d", &w);
if (m == 1) {
add(S, T, w); add(T, S, w);
continue;
}
int u = id(i, j, 1), v = id(i, j - 1, 0);
if (j == 1) {
add(u, S, w); add(S, u, w);
}
if (j == m) {
add(v, T, w); add(T, v, w);
}
if (j != 1 && j != m) {
add(u, v, w); add(v, u, w);
}
}
}
for (int i = 1; i < n; i++) {
for (int j = 1, w; j < m; j++) {
scanf("%d", &w);
int u = id(i, j, 0), v = id(i, j, 1);
add(u, v, w); add(v, u, w);
}
}
Dijkstra(T);
printf("%d\n", dis[S]);
return 0;
}